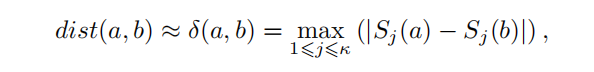路网嵌入是一种用来计算最短道路距离的方案,通过记录每个节点(道路之间的交叉口)的信息,把常规的道路用多维空间向量表示,使得每个节点之间的距离更能更有效地被计算。
介绍
路网嵌入是一种用来计算最短道路距离的方案,通过记录每个节点(道路之间的交叉口)的信息,把常规的道路用多维空间向量表示,使得每个节点之间的距离更能更有效地被计算。
Road Network Embedding (RNE), proposed by Shahabi et al.* [12], is an approach to compute shortest path distance in road networks, which bases on the LLR embedding techniques [19]. RNE transforms a road network into a higher dimensional space by assigning a sketch (i.e., a vector) to every node such that the distance between any two nodes can be efficiently approximated using only their sketches.
主要步骤
(1) 设G=(V,E)为路网(road network)
V代表道路之间的交叉节点,E(edge)代表道路。
(2) V有n个,把V分成n个子集如下
V : R = {V1,1, . . . , V1,α, . . . , Vβ,1, . . . , Vβ,α}
Let n = |V | be the size of the node set V . Define R as a set of O(log2n) reference sets, which are subsets of V : R = {V1,1, . . . , V1,α, . . . , Vβ,1, . . . , Vβ,α}, where α = O(log n) and β = O(log n).
Each subset Vi,ji is defined as a random subset of V with 2i nodes randomly chosen from V .
(3) 一个节点到一个子集Vij的距离即该节点到这个子集的最近距离所有节点距离的最小值
The distance between node v and subset Vi,j is defined as dist(v, Vi,j ) = minw∈Vi,j dist(v, w)
(4) 对于一个节点,把其到每个子集的最短距离记录下来,构成一个S集,这个S集就是该节点的路网嵌入向量,然后我们把所有的向量放在一起,构成路网嵌入数据集。

(5) 假设一个点u,处于节点s和t之间,该节点u到某个子集Vij之间的距离可以如下公式计算,
dist(u,s)为点u到节点s的距离,dist(u,t)同理。
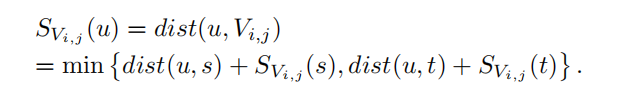
(6) 根据上面的分析,对于该点u,我们也可以得到一个路网嵌入向量如下
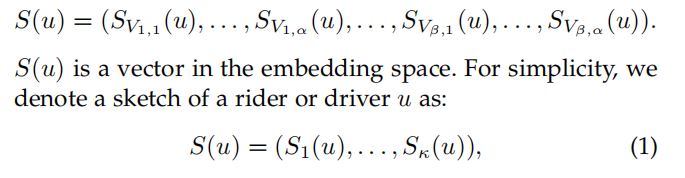
(7) 最终,我们可以计算任意两点a,b的最短距离