
概论
算法是啥?
为解决某一问题定义的计算过程。
是通过一个有限的指令序列集合对特定问题进行求解的一种计算执行描述。
算法的性质
可行性:可通过基本运算有限次执行来实现。
有穷性:算法的运行步数是有穷(即能运行完出结果的算法,运行不完没有结果有你有何用)
确定性:无二义性。
有输入输出:存在数据处理
程序与算法的区别
算法的概念与程序十分相似,但实际上有很大不同。程序并不都满足算法所要求的上述特征, 例如有限性特征。算法代表了对特定问题的求 解,而程序则是算法在计算机上的实现。
算法复杂度
- O;f/g=/=∞
举例
二分搜索复杂度为:O(logn)
合并两已排序表:O(n) n/2->n-1
选择排序:O(n^2) n(n-1)/2
插入排序:O(n^2) 最好n-1次,最坏n(n-1)/2
合并排序算法:O(nlogn)
时间复杂度
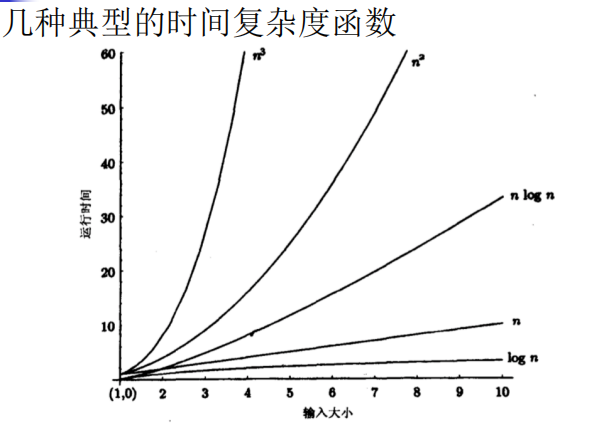
(1)O符号-上界
G越小越好
假设: f (n) 和g(n) 是从自然数集到非负实数集里的两个函数
定义1 (O):如果存在正的常数C和自然数n0,使得当n≥n0时, 有f(n)≤C·g(n),则称函数f (n) 在n 充分大
时有上有界,且g(n) 是它的一个上界,记做f (n) = O(g(n))
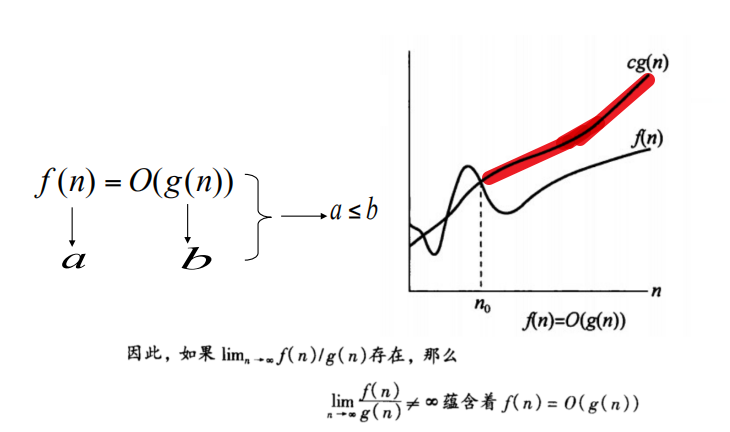
(2)Ω符号-下界
G越小大越好
定义2(Ω): 如果存在正的常数C 和自然数n0 , 使得当n ≥ n0时, 有f(n)≥C·g(n),则称函数f (n) 在n 充分大时有下有界,且g(n) 是它的一个下界,记做f (n) = Ω(g(n))
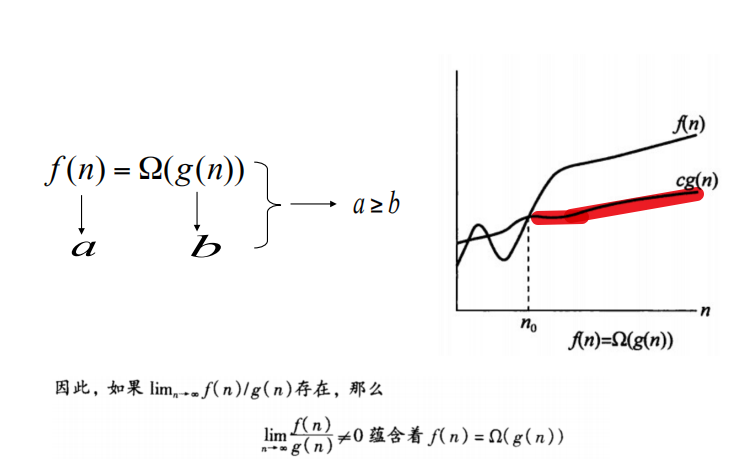
(3)Θ符号-渐进紧确界
最棒的表述,比O,Ω好
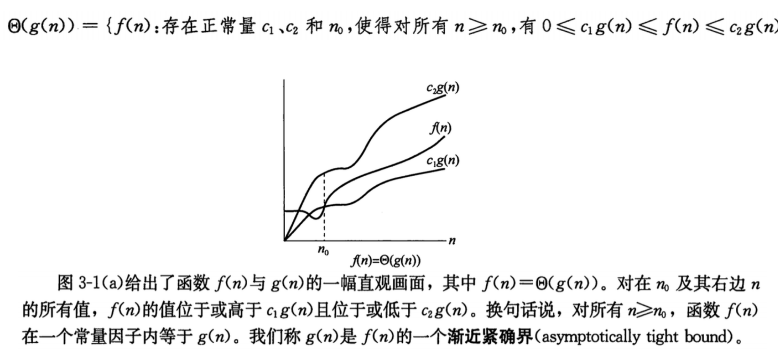

(4)o符号
与大O符号类似,但是大O符号对于某个大于零的常量c成立,而小o符号则对所有常量c>0成立

(5)性质
传递性:f<g<h;自反性:f=f;对称性:Θ相同;转置对称:f<g==g>f
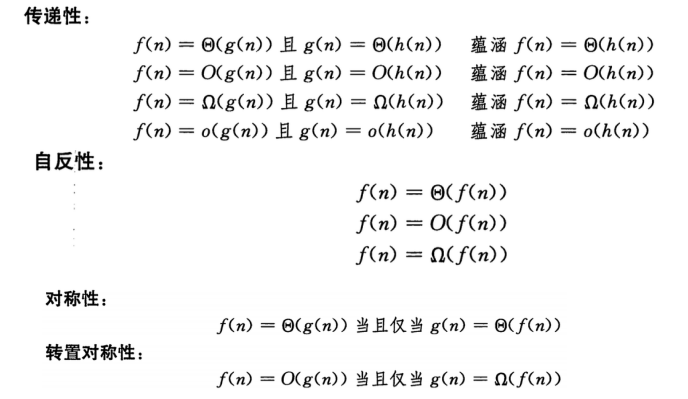
小问题
就是说不能说至少

估计算法时间复杂度
- 估计迭代次数
- 频度分析
- 使用递归方程
数学工具
- 数学基础
- 证明方法
- 直接证明、间接证明
- 反证法
- 数学归纳法
- 递归方程求解(*)
- Master定理(*)
- 基本数据结构
(1)证明方法
反证法

数学归纳法

(2)递归方程求解
常系数递归方程求解
T有n个就是n-1阶
T(n)=T(n-1)+T(n-2)有2阶


例子:
- 先弄出二阶方程、算出两个根
- 选择T(n)的表示法
- 根据题目给的两个T(n)的值计算C1、C2
- 最后代入(2)算出T(n)的表达式\即时间复杂度
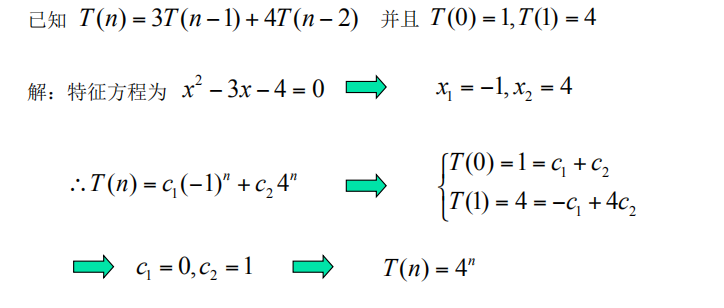
(3)Master定理

证明:
例子:
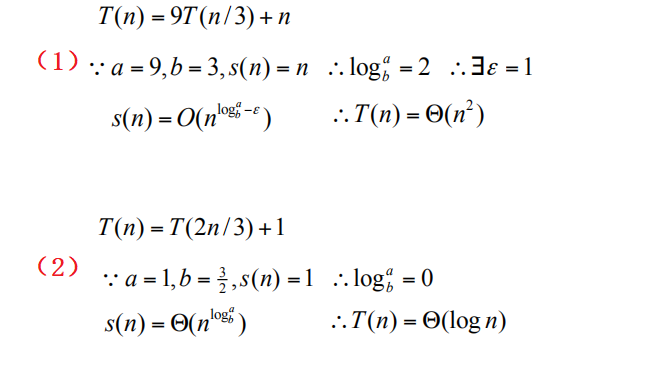
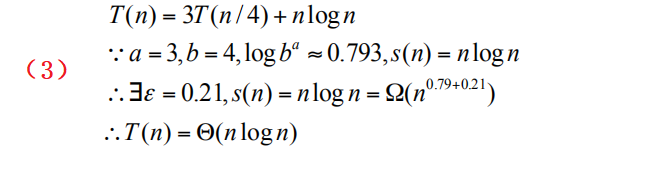
3/4*Log(n/4)<c *log(n)(c<1,随便取)
练习:

S(n)=O(n^(1/2-E)) E>0 E取0到1/2

S(n)=欧米伽(n^(1/2+E)) E>0 E取0到1/2
2*n/4< c *n c<1 取1/2<c<1