数学之美

《数学之美》是人民邮电出版社于2012年5月出版的图书，作者吴军，2014年再版。书中将高深的数学原理讲得更加通俗易懂，让非专业读者也能领略数学的魅力。通过具体实例教会读者在解决问题时如何化繁为简，如何用数学去解决工程问题，如何跳出固有思维不断去思考创新等。

第九章 图论和网络爬虫

图论定义

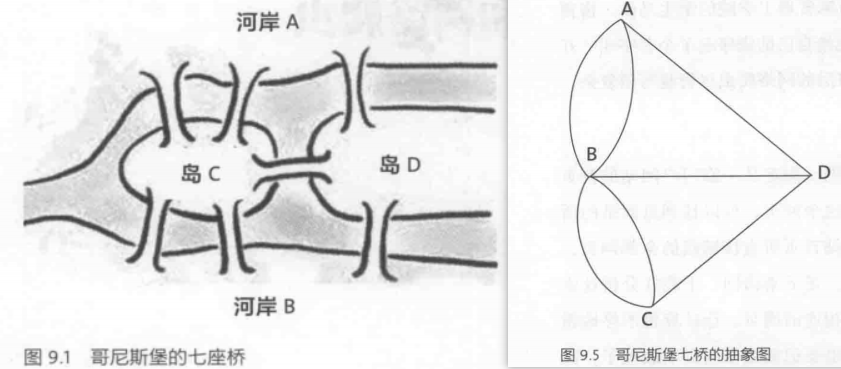
七桥问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点。

后来大数学家欧拉把它转化成一个几何问题——一笔画问题。在解答问题的同时，开创了数学的一个新的分支——图论与几何拓扑，也由此展开了数学史上的新历程。

PS：连通图可以一笔画的充要条件是：奇点的数目不是0 个就是2 个。

BFS广度优先遍历

爬虫用到了图论的遍历（Traverse）算法

BFS广度优先遍历（Breadth-First Search）算法如下

1. 初始只有一个已有节点
2. 遍历当前已有节点的邻接节点，加入已有节点
3. 重复步骤（2）直到不再有新的已有节点

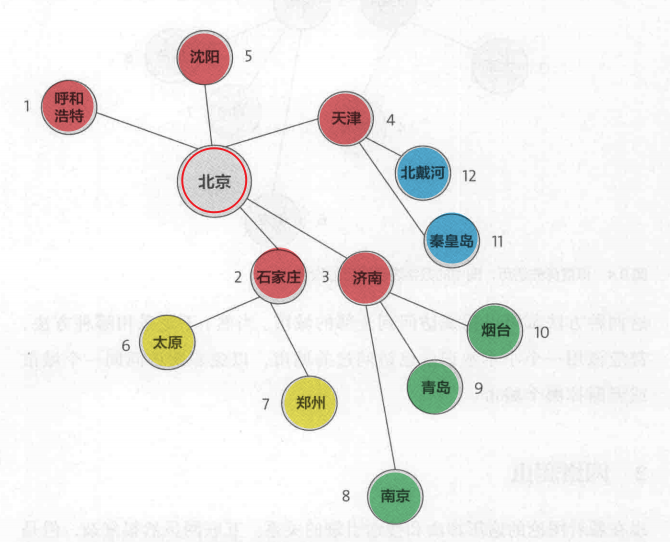
广度遍历的次序图（从北京开始）

DFS深度优先遍历

DFS深度优先遍历（Depth-First Search）算法如下

1. 初始只有一个未被标记节点
2. 查找未标记的节点的邻接节点A，找到节点A被标记
3. 进入该节点A第一个未标记的邻接节点B,将其设为A
4. 回到2直到所有节点遍历完

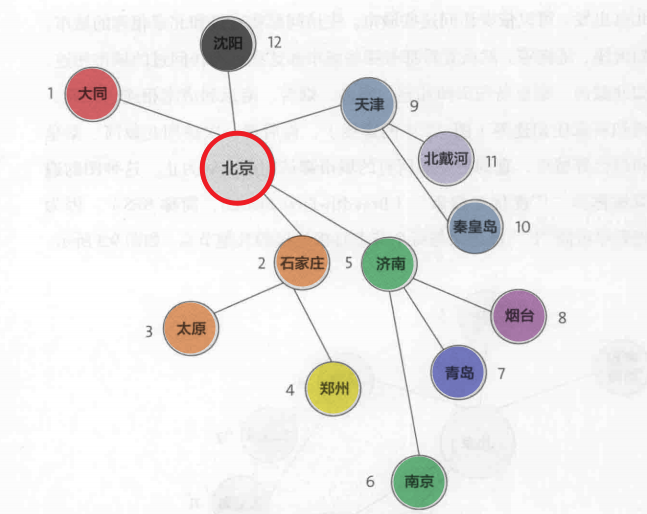
深度遍历的次序图（从北京开始）

网络爬虫(Web Crawlers）定义

• 互联网-就是一张大网（图）
• 一个网页为一个节点 node
• 网页中的超链接是一条边 edge，连向其他节点（网页）
• 网络爬虫正是遍历（访问）这张网并且下载网页（获得信息）的程序
• 使用哈希表（Hash Table）来记录一个网页是否被访问
• 现在的Google等公司使用的爬虫程序都是并行的、多设备，需要好的并行算法

搭建爬虫工程要点

• 用什么遍历算法？
• 页面的分析和URL的提取？
• URL记录表 已遍历哈希表的并行问题

1.用什么遍历算法？

一般来说，为了快速遍历重要的网址（比如腾讯主页中URL），用BFS

而为了减少目标服务器消耗（如TCP连接的握手次数过多，下载效率降低），用DFS

但是一般都没这么简单，需要一个复杂的复杂的调度系统Scheduler，工程上使用优先级队列与BFS类似

2.页面的分析和URL的提取？

由于很多网页HTML都是用脚本语言javascript来生成的（或逻辑控制，数据嵌入），所以一个HTML中的URL并不是显而易见的，需要通过浏览器渲染（运行javascript），所以一个好的爬虫需要熟悉浏览器内核的人来编写。

3.URL记录表 已遍历哈希表

由于一个URL可能被很多网页超链接。

如果爬虫足够大，爬取URL太多，那么在上千台服务器中，这个遍历哈希表就会变得相当大，维护很困难。这里的维护指的是哈希表的同步（避免重复下网页发生冲突）、存储（会大的一台服务器都存不下）

使用如下两种手段来控制

• 明确分工、如指定某个域名由某台机器爬取
• 把哈希表存储在一组独立的服务器上

小结

感受

之前在数据结构、离散数学中都学过图论，但是当时都是学了一遍便忘了。

直到近期在做一个项目，设计到了图论的遍历、最短路径问题。

才知道图论是如此的有意思，而这次看爬虫也是图论，算是再复习下吧，数学不愧是万物之源啊。

第十章 PageRank（网页排名）

网页排名是对搜索结果的分析，使那些更具“重要性”的网页在搜索结果中的排名获得提升，从而提高搜索结果的相关性和质量。

Google的page rank

核心思想

如果一个网页被其他网页所链接（投票），说明其受到了普遍的承认和信赖，那么此网页的Rank排名就高。

算法细化

对每个网页的 投票权重 做区分（就如股东大会的表决权）

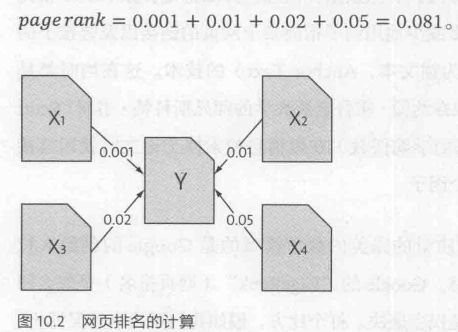
理论

将Pagerank用向量表示，并且用矩阵相乘的方法来迭代计算Pagerank。

初始的排名从哪来？全部设为1/n

（够暴力吧，理论证明，无论初值如何取，这种算法都能保证网页排名能收敛到真实值，无需人工干预）

实际问题

矩阵过于大计算量大，使用稀疏矩阵的计算技巧。

目前的发展

当今影响搜索引擎的质量的有如下几点：

• 好的索引库，如果一个URL没被索引，它就不可能被查到。

• 网页的质量的度量，如pagerank。

  目前的搜索引擎算法对网页质量的衡量复杂多了，是全方位的，质量的衡量以考用户点击等数据。

  顺带一提：因为google拥有的庞大数据积累，使得后来的搜索引擎无法超过他。而当年google刚成立时，pagerank算法的专利保护很好的保护了它度过了前期的数据积累时期。

  数据也是一种资本，这导致了，即使你现在做一个比百度还好的算法，却不可能替代它在国内的地位了。

• 用户偏好。用户的喜好不同推送不同的内容。

  目前的B站、知乎、淘宝的推荐都是用机器学校来判断你的喜好类型。这里批评一下，目前的推荐都是单调（只有个人的喜好）、且更新过于恶心（新类型的权重会很大，导致下次刷新都是该类型）。

• 与用户搜索的相关性。如果是做个人站的搜索，用TF-IDF就可以满足要求，而大公司的相关性判断则复杂的多。

  TF-IDF（term frequency–inverse document frequency）是一种用于信息检索与数据挖掘的常用加权技术。TF意思是词频(Term Frequency)，IDF意思是逆文本频率指数(Inverse Document Frequency)。

  一篇文章的相关性分数：TF*IDF。

第十八章 搜索引擎反作弊及搜索结果权威性

搜索引擎的反作弊

作弊SEO是伴随着搜索引擎排名产生的。搜索结果排名靠前的不一定是高质量的相关网站。

常见的作弊手段：针对tf-idf的重复关键词、针对PageRank的链接站（专业买卖链接URL）。

关于落地页（LandinPage），其内容质量高，但是里面暗藏js跳转，一进去就跳转到一个商业网站。

反作弊的哲学：一般小的搜索引擎没有作弊不是因为他们反作弊很好，而是因为作弊商看不上这些小站。

如何反作弊

抓作弊成为了“猫捉老鼠”的游戏，没有一劳永逸的方法（信息安全也是如此）。

透过具体问题，看本质和动机，解决问题。反作弊也是如此，需要“道”。术即是表层，道即事物本质。

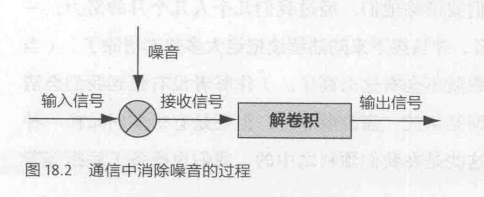
而通信模型对于搜索反作弊依然适用。在通信中解决噪声干扰问题的基本思路有两条。

• 从信息源出发，加强通信（编码）自身的抗干扰能力。
• 从传输来看，过滤掉噪声，还原信息。

如下图，原始的信号混入噪声，在数学上表现为他们两个做了卷积，消除噪声的过程就是解卷积的过程。

反作弊中”道“的扩展

一个判断链接站的思路：

将网站的出链（其指向的URL）作为一个向量，它是这个网站的固有特征。

而通过对两个网站的向量计算余弦距离，若两个网站的出链URL几乎相同，则其出链向量的余弦距离为几近于1。

另一个判断链接站的思路：

由于链接站普遍两两链接，所以使用图论来寻找这些互联网中的闭环，就可以找到链接站。

可以看到，这两个思路都用到了数学，赞美数学！

搜索结果的权威性

权威性：例如医疗方面的问题，需要判断搜索结果是否完全可信，这就是权威性的判断。

如何判断权威性呢？

一个概念 “提及”（Mention）。

如果一个主题中的信息页中，有某个机构普遍、多次被“提及”，那就有理由判断其是权威的。

计算权威有两个难点：

• “提及”需要自然语言处理NLP（natural language processing），得知文本内容的意思。
• 权威是与领域相关的，一个机构在医学领域是权威的，但其在其他领域不一定相关。

权威性计算

1. 句法分析，寻找涉及主题短语、对信息源的描述。
2. 利用互信息，寻找道主题短语和信息源的相关性。
3. 对主题短语进行聚类，这里需要用到NLP，比如”吸烟的危害“和”香烟的危害“是相同的。
4. 一个网站也要分成不同的领域来判断。

（句法分析、互信息、聚类后面都是数学!）

总结

虽然先前都有了学习，但是看了这几章，还是不得不赞叹数学、信息论的力量。

从网络爬虫中的图论知识，到PageRank中的矩阵运算，TF-IDF、反作弊中余弦、闭环的巧妙运用等等。

都是数学的应用体现，麻麻再也不担心我讨厌数学了。

收获还是有的吧，爬虫和pagerank课上都学过了，这里权当复习了。

而互联网为啥叫网，我终于清晰的了解了。反作弊我还是第一次学习到，很有趣。

在互联网时代，学这些是有好处的，毕竟网络已经无处不在，学这些有利于“生存”。