信息内容安全实验2

发表于 | 分类于
字数统计: 6.3k字 | 阅读时长 ≈ 25分钟

image-20200409163141122

[TOC]

实验环境

IDE：pycharm

python版本：anacoda->python3.7

实验1.1-分词与词向量化

背景介绍

1.分词

对于西方拼音语言来讲，词之间有明确的分解符，统计和使用语言模型非常直接，而对于中文，词之间没有明确的分界符。因此需要对句子分词后，才能做自然语言处理。

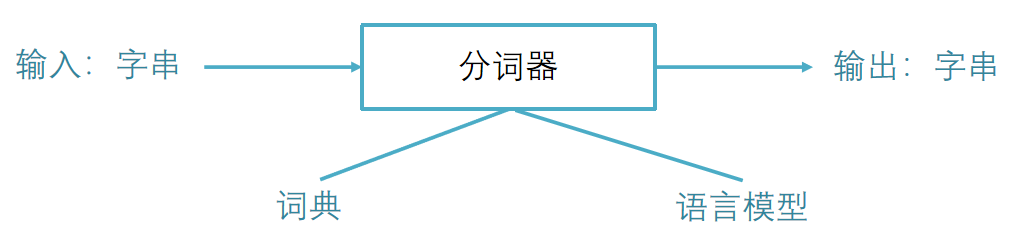
image-20200409164613616

Python中分分词工具很多，包括盘古分词、Yaha分词、Jieba分词等。

这里选择Jieba（结巴）分词作为我们实验的工具

安装

1
pip install jieba

常用方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#导入自定义词典  
jieba.load_userdict(“字典路径\名称.txt")  
#动态修改词典              
add_word(word, freq=None, tag=None)
del_word(word) 
#可调节单个词语的词频，使其能（或不能）被分出来
suggest_freq(segment, tune=True) 
#关键词提取
#sentence 为待提取的文本; topK默认值是20; 
#withWeight 为是否一并返回关键词权重值，默认值为 False; allowPOS 仅包括指定词性的词
jieba.analyse.extract_tags(sentence, topK=20, withWeight=False, allowPOS=())
#添加停用词
jieba.analyse.set_stop_words(“extra_dict/stop_words.txt”)
基于textrank的关键词提取
tags = jieba.analyse.textrank(text, topK=5, withWeight=False, allowPOS=('ns', 'n', 'vn', 'v'))

2.词向量化

自然语言理解的问题要转化为机器学习的问题，第一步肯定是要找一种方法把这些符号数学化。

NLP 中最直观，也是到目前为止最常用的词表示方法是 One-hot Representation。

这种方法把每个词表示为一个很长的向量。

这个向量的维度是词表大小，其中绝大多数元素为 0，只有一个维度的值为 1，这个维度就代表了当前的词。

​ 举个例子：

​ “话筒”表示为 [0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 …]

​ “麦克”表示为 [0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 …]

每个词都是茫茫 0 海中的一个 1。

！但是这种简单的方法有两个缺点：
1.维数灾难
2.“词汇鸿沟”现象：任意两个词之间都是孤立的，无法判断像“话筒”和“麦克”是同义词。

所以，我们需要词向量表示

新的词表示方法叫做Distributed Representation（分布式表示）。

这种方法表示词即用一个地位实数向量来表示一个词，如：[0.792, −0.177, −0.107, 0.109, −0.542, …]

语言进行词向量化，可使用Word2Vec。

word2vec是google的一个开源工具，能够根据输入的词的集合计算出词与词之间的距离。

它将term转换成向量形式，可以把对文本内容的处理简化为向量空间中的向量运算。

计算出向量空间上的相似度，来表示文本语义上的相似度。

word2vec计算的是余弦值，距离范围为0-1之间，值越大代表两个词关联度越高。

安装

1
2
3
4
5
6
#安装带mkl的版本，下载wheel文件
http://www.lfd.uci.edu/~gohlke/pythonlibs
#定位到存放.whl文件的文件夹，通过匹配安装对应版本的numpy 和scipy
pip install numpy-1.12.1+mkl-cap36
#安装完后，继续安装genism
pip install -U gensim

为了减少安装中的繁琐，直接在anaconda进行集中安装，安装：

1
pip install gensim

实验

1.分词

代码如下，主要的都写了注释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# encoding=utf-8
import codecs
import os
import jieba
import jieba.analyse

# 导入自定义词典
jieba.load_userdict("dict_all.txt")
# 读入语料库并且分词
def read_file_cut():
    # 语料库路径
    pathBaidu = "BaiduSpiderCountry\\"
    # 分词结果
    resName = "Result_Country.txt"
    if os.path.exists(resName):
        os.remove(resName)
    result = codecs.open(resName, 'w', 'utf-8')

    num = 1
    while num <= 100:  # 5A 200 其它100
        name = "%04d" % num   #文件遍历格式：0001->0100
        fileName = pathBaidu + str(name) + ".txt"  #
        source = open(fileName, 'r',encoding="utf-8")  #打开文件
        line = source.readline()     #获得line迭代器

        while line != "":
            line = line.rstrip('\n')  # 删除string字符串末尾的指定字符
            seglist = jieba.cut(line, cut_all=False)  # 精确模式
            output = ' '.join(list(seglist))  # 空格拼接，将元组转换为列表，元组是括号，列表是方括号
            result.write(output + ' ')  # 空格取代换行'\r\n'
            line = source.readline()   #下一line
        else:
            print('End file: ' + str(num))  #line为空，这个文件遍历结束
            result.write('\r\n')  #换行'\r\n'
            source.close()        #关闭源
        num = num + 1  #下一个文件
    else:
        print('End BaiduSpiderCountry cut：'+str(num)) # 结束百度语料库分词

# Run function
if __name__ == '__main__':
    read_file_cut()

换行格式：

1、文档是windows格式，当我们按下键盘上的“回车键”时，输出的是CR和LF，即0d，0a两个字符。
2、文档是unix格式，当我们按下键盘上的“回车键”时，输出的LF，即0a一个字符。
3、文档是mac模式，当我们按下键盘上的“回车键”时，输出的是CR，即0d一个字符。

运行~

成功

image-20200409184925832

分词结果如下

image-20200409184959263

1.词向量化

代码如下，主要的都写了注释

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from gensim.models import word2vec
import  logging

# 初始化配置
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
# 加载语料
sentences = word2vec.Text8Corpus("Result_Country.txt")
# 训练模型,维度设置为200;
model = word2vec.Word2Vec(sentences, size=200) 

print("阿富汗的词向量：")
print(model['阿富汗'])

print("争端、冲突这两个词的相关程度：")
y1 = model.similarity("争端","冲突")
print(y1)

print("输出与“地区”相关度最高的20 个词：")
y2 = model.most_similar("地区", topn=20)
print(y2)

print("法官 总统 部长 北纬 这四个词中最“不合群”的词")
y4 = model.doesnt_match("法官 总统 部长 北纬".split())
print(y4)

#保存模型
model.save("国家.model")
# 读取模型
# model_2 = word2vec.Word2Vec.load("国家.model")

运行

模型跑成功

image-20200409190406516

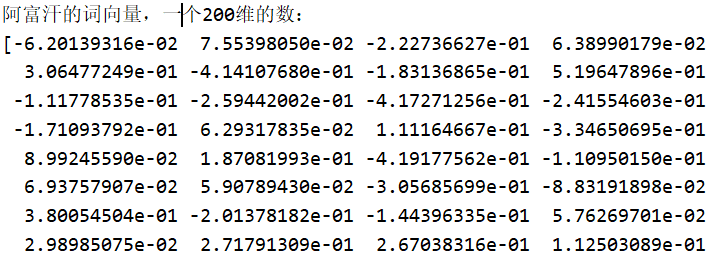
  • 阿富汗的词向量，一个200维的数：

​ image-20200409192647571

  • 争端、冲突这两个词的相关程度：

image-20200409192713430

  • 输出与“地区”相关度最高的20 个词：

image-20200409192810184

  • 法官 总统 部长 北纬 这四个词中最“不合群”的词

image-20200409192855779

保存模型

image-20200409193001889

实验1.2-自选词典数据语料库

1.选择词典数据语料库

  • 在词典方面，我用搜狗的细胞词库
  • 在语料库方面，我选择BBC语料库
    • 如图，在科技板块，搜索相关关键词
    • image-20200411180437845
    • 大概搜索了五个关键词（如病毒、蠕虫、网络安全等）。
    • 然后根据其语料集存在的问题，进行数据清洗

选择词典数据语料库的结果如下

image-20200411180819848

2.分词

代码与第一个实验基本一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
def security_cut():
    # 导入自定义词典
    jieba.load_userdict("security_dict.txt")
    # 语料库路径
    pathBaidu = "security\\"
    # 分词结果
    resName = "Result_Security.txt"
    if os.path.exists(resName):
        os.remove(resName)
    result = codecs.open(resName, 'w', "utf-8")

    num = 1
    while num <= 5:  # 5A 200 其它100
        name = "%d" % num   #文件遍历格式：0001->0100
        fileName = pathBaidu + str(name) + ".txt"
        source = open(fileName, 'r',encoding="utf-8")  #打开文件
        line = source.readline()     #获得line迭代器

        while line != "":
            line = line.rstrip('\n')  # 删除string字符串末尾的指定字符
            seglist = jieba.cut(line, cut_all=False)  # 精确模式
            output = ' '.join(list(seglist))  # 空格拼接，将元组转换为列表，元组是括号，列表是方括号
            result.write(output + ' ')  # 空格取代换行'\r\n'
            line = source.readline()   #下一line
        else:
            print('End Security file: ' + str(num))  #line为空，这个文件遍历结束
            result.write('\r\n')  #换行'\r\n'
            source.close()        #关闭源
        num = num + 1  #下一个文件
    else:
        print('End Security cut') # 结束百度语料库分词
# Run function
if __name__ == '__main__':
    security_cut()

3.词向量化

代码与第一个实验基本一致

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# This Python file uses the following encoding: utf-8
from gensim.models import word2vec
import  logging

# 初始化配置
logging.basicConfig(format='%(asctime)s : %(levelname)s : %(message)s', level=logging.INFO)
# 加载语料
sentences = word2vec.Text8Corpus("Result_Security.txt")
# 训练模型,维度设置为200;
model = word2vec.Word2Vec(sentences, size=200)

print("病毒的词向量，一个200维的数：")
print(model['病毒'])

print("病毒、木马这两个词的相关程度：")
y1 = model.similarity("病毒","木马")
print(y1)

print("输出与“网络安全”相关度最高的20 个词：")
y2 = model.most_similar("网络安全", topn=20)
print(y2)

print("病毒 木马 诺顿 蠕虫 这四个词中最“不合群”的词")
y4 = model.doesnt_match("病毒 木马 诺顿 蠕虫".split())
print(y4)

#保存模型
model.save("网络安全.model")
# 读取模型
# model_2 = word2vec.Word2Vec.load("国家.model")

词向量模型训练成功，测试的结果如下

  • 病毒的词向量，一个200维的数：

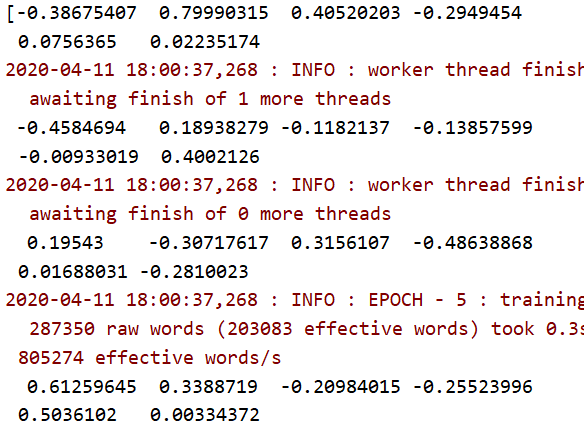
    image-20200411181124453

  • 病毒、木马这两个词的相关程度：0.9492484

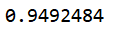
    image-20200411181203044

  • 输出与“网络安全”相关度最高的20 个词：

    image-20200411181231329

  • 病毒 木马 诺顿 蠕虫 这四个词中最“不合群”的词：诺顿

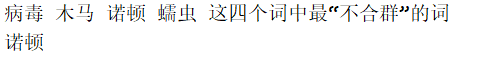
    image-20200411181303308

#coding = gbk

实验2-垃圾邮件的分类

原理

1.文本分类

文本分类就是在给定的分类体系下,让计算机根据给定文本的内容，将其判

别为事先确定的若干个文本类别中的某一类或某几类的过程。

一般来说，文本分类可以分为一下过程：

（1） 预处理：将原始语料格式化为同一格式，便于后续的统一处理；

（2） 索引：将文档分解为基本处理单元，同时降低后续处理的开销；

（3） 统计：词频统计，项（单词、概念）与分类的相关概率；

（4） 特征抽取：从文档中抽取出反映文档主题的特征；

（5） 分类器：分类器的训练；

（6） 评价：分类器的测试结果分析。

典型的分类算法包括Rocchio算法、朴素贝叶斯分类算法、K-近邻算法、决

策树算法、神经网络算法和支持向量机算法等。

2.朴素贝叶斯分类算法

根据贝叶斯定理，利用先验概率和条件概率估算后验概率：

先验概率：事情还没有发生,那么这件事情发生的可能性的大小。

后验概率：事情已经发生,那么这件事情发生的原因是由某个因素引起的可能性的大小。

image-20200416153013132

将该算法代入我们的垃圾邮件分类任务中之后，理论如下：

(1).概率计算

假设c0是正常邮件，c1是垃圾邮件。𝑝(𝑐0)表示在邮件数据集中，正常邮件的概率，𝑝(𝑐1)则表示垃圾邮件的概率，所以计数之后除以邮件总数即可。

x与y分别是邮件的两个特征，那么，当邮件有x和y两个特征时（因为两个概率的分母完全一样，因此在比较两者大小时可忽略分母。）

  • 为正常邮件的概率为𝑝(𝑐0/𝑥, 𝑦) =𝑝(𝑥, 𝑦/c0)*p(c0)

  • 为垃圾邮件的概率为𝑝(𝑐1/𝑥, 𝑦) =𝑝(𝑥, 𝑦/c1)*p(c1)

(2).“朴素”——引入条件独立性假设

x和y的条件概率相互独立。𝑝(𝑥/𝑐𝑖)和𝑝(𝑦/𝑐𝑖)可以对数据进行计数而直接得出。

则条件概率𝑝(𝑥, 𝑦/ci)=𝑝(𝑥/c0)*𝑝(𝑦/ci)

即上述公式为𝑝(𝑐0/𝑥, 𝑦) =𝑝(𝑥, 𝑦/c0)*𝑝(c0)=𝑝(𝑥/c0)*𝑝(𝑦/ci)*p(c0)

(3).假设每个样本至少出现一次

由于条件独立性假设，需要对条件概率进行乘法运算，若某个样本不出现，即概率为0，则最后结果也为0。所以假设每个样本至少出现一次。

(4).将全部乘法运算改为log运算

在实际运算中，条件概率可能会很小，即接近于0，那么在乘法运算中很可能会有下溢出的问题。

3.实际的编码流程

在本实验中，实际的编码时，我们所需要做的事按顺序排列的如下：

  1. 网上选择一些中文常用的停用词。

  2. 读入spam（恶意）、ham（正常）邮件，用jieba.cut()分词，并且去除停用词，保存。

  3. 用jieba.analyse.extract_tags()分别提取两个文件的前50（或更多）常见词，合成为一个常见词list，作为我们的特征词向量features。

  4. 接下来，对spam、ham的分词结果进行特征词向量features的特征计算：

    1. 对每一封邮件，其特征词向量features全为1
    2. 统计其在features中每个词的出现次数
    3. 如果features出现一次，该项就加1

  5. 根据朴素贝叶斯定理计算spam、ham后验概率spam_vec\ham_vec

  6. 计算spam、ham各占总邮件数的概率p_spam、p_ham

  7. 计算待测试集的特征集向量test_vec

  8. 将test_vec*spam_vec*p_spam 与test_vec*ham_vec*p_ham相比，

  9. 哪方概率大则该封测试邮件属于哪一类（为了避免正常邮件分为垃圾邮件，当概率相等时，判定为正常）

代码

  1. 网上选择一些中文常用的停用词。

image-20200416161709427

  1. 读入spam（恶意）、ham（正常）邮件，用jieba.cut()分词，并且去除停用词，保存。

  2. 用jieba.analyse.extract_tags()分别提取两个文件的前50（或更多）常见词，合成为一个常见词list，作为我们的特征词向量features。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def extract_tags_f(origin_file_name, target_file_name,number_of_item):
    stop_word_file = "stop_word_list.txt"  # 停用词txt
    stop_word = list()  # 停用词数组
    target_file = open(target_file_name, "w", encoding="utf-8")  # 提取保存的文件
    with open(stop_word_file, 'r', encoding="utf-8") as stop_word_file_object:
        contents = stop_word_file_object.readlines()
        # print(contents)
        for line in contents:
            line = line.strip()  # 移除尾部字符
            stop_word.append(line)
    # print(stop_word)
    origin_file = origin_file_name #对文件进行逐行遍历分词
    s = "" #没有停顿词的文件中每一行的词串
    with open(origin_file, 'r', encoding="utf-8") as origin_file_obejct:
        contents = origin_file_obejct.readlines() #读取
        # print(contents)
        for line in contents:
            line = line.strip() #将line去除尾部回车换行
            out_line = "" #处理后的line
            word_list = jieba.cut(line, cut_all=True) #分词成list
            for word in word_list:  #将list以空格间隔合并
                if (word not in stop_word) and (word != "\t"): #去除停用词
                    out_line = out_line + word + " "
            s = s + out_line #没有停顿词的文件中每一行的词串
            target_file.write(out_line.strip() + "\n") #保存分词文件
    # print(s)
    features = jieba.analyse.extract_tags(s, number_of_item) #将分词特征提取
    # print(features)
    # print(len(features))
    return features
  1. 接下来，对spam、ham的分词结果进行特征词向量features的特征计算：
    1. 对每一封邮件，其特征词向量features全为1
    2. 统计其在features中每个词的出现次数
    3. 如果features出现一次，该项就加1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
def calc_vec(ham,spam,features):
    with open(ham, 'r', encoding="utf-8") as f1:
        ham_lines = f1.readlines()
    with open(spam, 'r', encoding="utf-8") as f1:
        spam_lines = f1.readlines()
    list_sum=np.zeros((200,len(features))) #所有特征词向量，前100为正常邮件，后100为垃圾邮件
    list_sum_i=0    #所有特征词向量的赋值下标i
    for i in ham_lines: #计算每封正常邮件特征词向量
        list_ham = np.ones(len(features)) #对每一封邮件，其特征词向量features全为1
        line = i.split(' ') #按空格split成一个邮件词list
        for j in range(len(features)): #对于features中每个词
            for line_feature in line : #统计邮件中每个词的出现次数
                if features[j] == line_feature: #如果features出现一次，该项就加1
                    # print("get")
                    list_ham[j]=list_ham[j]+1
        list_sum[list_sum_i]=list_ham #将该封邮件词向量复制给所有特征词向量
        list_sum_i +=1
    # print("——————————————————————————————————————————————————————")
    for i in spam_lines: #计算垃圾邮件特征词向量
        list_spam = np.ones(len(features))
        line = i.split(' ')
        for j in range(len(features)):
            for line_feature in line :
                if features[j] == line_feature:
                    # print("get")
                    list_spam[j]=list_spam[j]+1
        list_sum[list_sum_i]=list_spam
        list_sum_i +=1
    cate1=[0]*100  #前面100封邮件正常，后面100封邮件垃圾
    cate2=[1]*100
    cate=cate1+cate2 #cate为邮件的类别lsit
    return list_sum,cate
  1. 根据朴素贝叶斯定理计算spam、ham后验概率spam_vec\ham_vec
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def traing_bayes(trainMatrix, trainCategory):  # trainMatrix为所有邮件的矩阵表示，trainCategory为表示邮件类别的向量
    import numpy as np
    numTrainDocs = len(trainMatrix)  # 邮件总数量
    numWords = len(trainMatrix[0])  # 词典长度
    pSpam = sum(trainCategory) / float(numTrainDocs)  # 统计垃圾邮件的总个数，然后除以总文档个数（先验概率）
    p0Num = np.ones(numWords)  # 将向量初始化为1，表示每个词至少出现1次
    p1Num = np.ones(numWords)  # 同上
    p0Denom = 2.0
    p1Denom = 2.0  # 分母初始化为2
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:  # 如果是垃圾邮件
            p1Num += trainMatrix[i]  # 把属于同一类的文本向量相加，实质是统计某个词条在该类文本中出现频率
            p1Denom += sum(trainMatrix[i])  # 把垃圾邮件向量的所有元素加起来，表示垃圾邮件中的所有词汇
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1 = np.log(p1Num / p1Denom)  # 统计词典中所有词条在垃圾邮件中出现的概率
    p0 = np.log(p0Num / p0Denom)  # 统计词典中所有词条在正常文邮件中出现的概率
    return p0,p1,pSpam
  1. 计算spam、ham各占总邮件数的概率p_spam、p_ham
  2. 计算待测试集的特征集向量test_vec
  3. 将test_vec*spam_vec*p_spam 与test_vec*ham_vec*p_ham相比
  4. 哪方概率大则该封测试邮件属于哪一类（为了避免正常邮件分为垃圾邮件，当概率相等时，判定为正常）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
def test_classify(test,features,ham_vec,spam_vec,p_spam):
    with open(test, 'r', encoding="utf-8") as f1:
        test_lines = f1.readlines()
    line_i=1 #用于判断计算到了第几封test，test集中，前50为正常，后50为垃圾
    TP=0 #正确肯定
    TN=0 #正确否定
    FP=0 #错误肯定
    FN=0 #错误否定
    for i in test_lines: #计算test集邮件的词向量，并且判断正常\垃圾
        test_vec = np.zeros(len(features))
        line = i.split(' ')
        for j in range(len(features)):
            for line_feature in line :
                if features[j] == line_feature:
                    test_vec[j]=test_vec[j]+1
        pnorm=sum(test_vec*ham_vec*p_spam)
        pabu=sum(test_vec*spam_vec*p_spam)
        # if (line_i == 47):
        #     print(test_vec)
        # if(line_i==51): #如果开始判断垃圾邮件就分下行
            # print("————————————————————————————————————————")
        if pnorm>=pabu : #正常概率大（ps:当概率相等时，判定为正常)
            if line_i>50 :
                # print("第%d封邮件是正常邮件" % line_i, end='')
                # print("————判断错误！————"+"其实是垃圾邮件哒!",end='')
                FP=FP+1
            else:
                # print("第%d封邮件是正常邮件" % line_i, end='')
                TP =TP+1
        else:
            if line_i < 51:
                # print("————判断错误！————" + "其实是正常邮件哒",end='')
                TN=TN+1
            else:
                # print("第%d封邮件是错误邮件" % line_i, end='')
                FN=FN+1
        # print("   正常概率VS错误概率：",end='')
        # print(pnorm,pabu)
        line_i+=1
    print("featuears项数：",len(features))
    print("正确肯定：预测为真，实际为真",TP)
    print("正确否定：预测为假，实际为真",TN)
    print("错误肯定：预测为真，实际为假",FP)
    print("错误否定：预测为假，实际为假",FN)
    P=TP/(TP/FP) #查准率
    R=TP/(TP+FN) #查全率
    ACC=(TP+FN)/(TP+TN+FP+FN)
    F = 2*TP / (2*TP+FP+FN)
    print("查准率P=TP/（TP+FP）:",P)
    print("查全率R=TP/（TP+FN）:",R)
    print("准确率ACC=(TP+FN) / (TP+TN+FP+FN):",ACC)
    print("调和均值F= 2TP / (2TP+FP+FN):",F)

main函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def main():
    number_of_item=[10,25,50,75,100,150,200,300,500]
    for i in number_of_item:
        print("————————————————————————————————————————")
        print("特征项数为：",i)
        extract_tags_f("test.utf8", "test_word.txt",i)  
        #对测试集分词
        features = extract_tags_f("ham_100.utf8", "ham_word.txt",i) 
        #对正常邮件分词，并提取词向量
        features += extract_tags_f("spam_100.utf8", "spam_word.txt",i) 
        #垃圾邮件分词，并提取词向量
        duplicated = set()
        for i in range(0,len(features)):
            if features[i] in features[i+1:]:
                duplicated.add(features[i]) 
                #寻找垃圾邮件和正常邮件重复的特征词
        # print(duplicated)
        for i in range(len(features) - 1, -1, -1):
            if features[i] in duplicated:
                features.remove(features[i]) 
                #去除垃圾邮件和正常邮件重复的特征词，但是感觉效果并不好
        # print(features)
        print("去除重复词后特征项数为：",len(features))
        list_sum,cate=calc_vec("ham_word.txt","spam_word.txt",features) #计算总体词向量
        ham_vec, spam_vec,p_spam=traing_bayes(list_sum,cate) #计算条件概率，以及先验概率
        test_classify("test_word.txt",features,ham_vec, spam_vec,p_spam) #分类

运行程序：

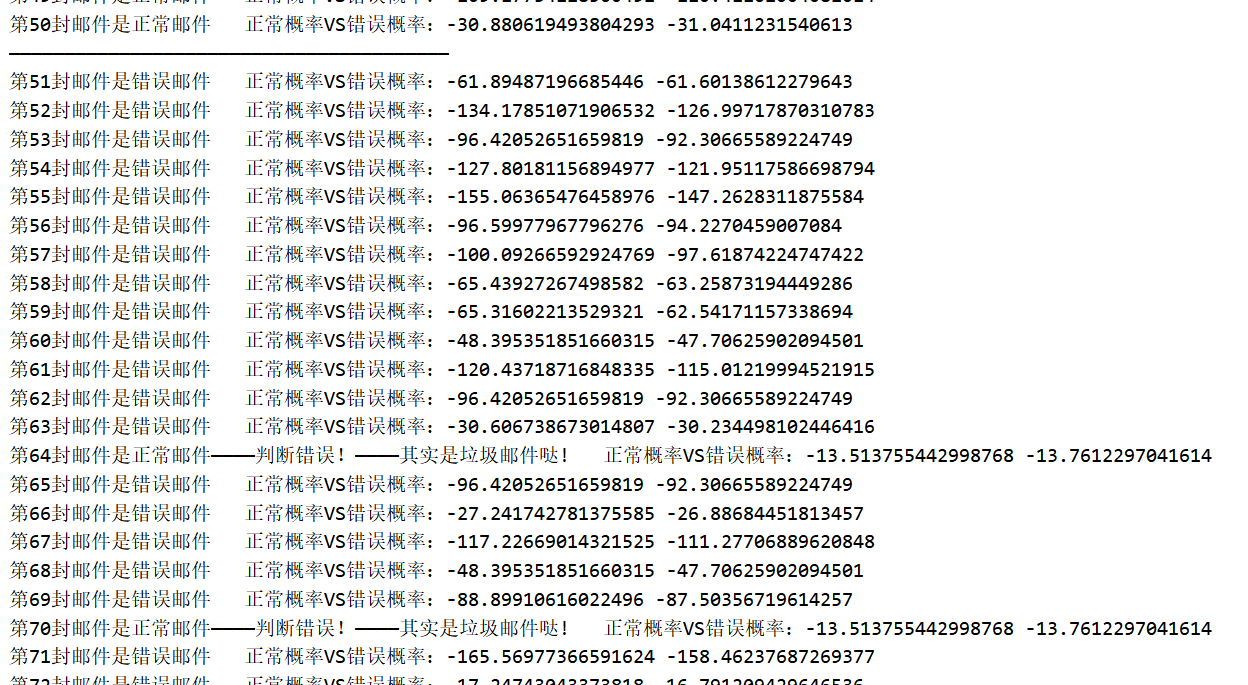
image-20200416165856310

总结

朴素贝叶斯分类算法评价：

查准率（Precision）、查全率（召回率）（Recall）、准确率(Accuracy)

我们将算法预测的结果分成四种情况：

  1. 正确肯定（True Positive,TP）：预测为真，实际为真

  2. 正确否定（True Negative,TN）：预测为假，实际为真

  3. 错误肯定（False Positive,FP）：预测为真，实际为假

  4. 错误否定（False Negative,FN）：预测为假，实际为假

则：

查准率P=TP/（TP+FP）

查全率R=TP/（TP+FN）

准确率ACC=(TP+FN) / (TP+TN+FP+FN)

以下为去除重读词

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
去除重复词后特征项数为： 20
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.86
调和均值F= 2TP / (2TP+FP+FN): 0.647887323943662
————————————————————————————————————————
去除重复词后特征项数为： 48
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.9
调和均值F= 2TP / (2TP+FP+FN): 0.6575342465753424
————————————————————————————————————————
去除重复词后特征项数为： 96
查准率P=TP/（TP+FP）: 10.0
查全率R=TP/（TP+FN）: 0.550561797752809
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.89
调和均值F= 2TP / (2TP+FP+FN): 0.6621621621621622
————————————————————————————————————————
去除重复词后特征项数为： 142
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.92
调和均值F= 2TP / (2TP+FP+FN): 0.6666666666666666
————————————————————————————————————————
去除重复词后特征项数为： 192
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.92
调和均值F= 2TP / (2TP+FP+FN): 0.6666666666666666
————————————————————————————————————————
去除重复词后特征项数为： 290
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.92
调和均值F= 2TP / (2TP+FP+FN): 0.6666666666666666
————————————————————————————————————————
去除重复词后特征项数为： 386
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.92
调和均值F= 2TP / (2TP+FP+FN): 0.6666666666666666
————————————————————————————————————————
去除重复词后特征项数为： 578
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.93
调和均值F= 2TP / (2TP+FP+FN): 0.6666666666666666
————————————————————————————————————————
去除重复词后特征项数为： 924
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.92
调和均值F= 2TP / (2TP+FP+FN): 0.6666666666666666

可以看到调和均值F趋近于极限了，再加特征项数也无用

如果不去除重读词，反而会好些，最好结果如下，特征项数为150

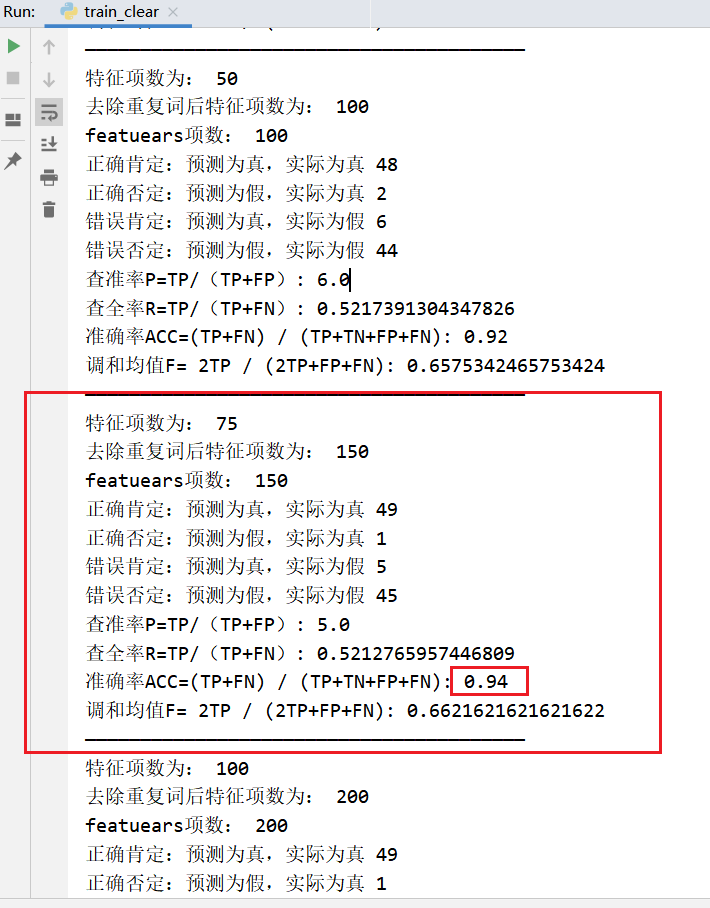
image-20200416171617463

1
2
3
4
5
6
7
8
9
10
11
特征项数为： 75
去除重复词后特征项数为： 150
featuears项数： 150
正确肯定：预测为真，实际为真 49
正确否定：预测为假，实际为真 1
错误肯定：预测为真，实际为假 5
错误否定：预测为假，实际为假 45
查准率P=TP/（TP+FP）: 5.0
查全率R=TP/（TP+FN）: 0.5212765957446809
准确率ACC=(TP+FN) / (TP+TN+FP+FN): 0.94
调和均值F= 2TP / (2TP+FP+FN): 0.6621621621621622

错误的基本是如下6封，不过如果去除重复词那就不会有将正常邮件判断成错误邮件的情况。

1
2
3
4
5
6
7
8
9
10
11
12
13
第29封邮件是错误邮件————判断错误！————其实是正常邮件哒   
正常概率VS错误概率：-44.397541630442696 -44.09868095860785
————————————————————————————————————————
第64封邮件是正常邮件————判断错误！————其实是垃圾邮件哒!   
正常概率VS错误概率：-13.513755442998768 -13.7612297041614
第70封邮件是正常邮件————判断错误！————其实是垃圾邮件哒!   
正常概率VS错误概率：-13.513755442998768 -13.7612297041614
第73封邮件是正常邮件————判断错误！————其实是垃圾邮件哒!   
正常概率VS错误概率：-6.9073094336244685 -6.939395461206766
第92封邮件是正常邮件————判断错误！————其实是垃圾邮件哒!   
正常概率VS错误概率：-54.79272850055003 -55.26584135501914
第94封邮件是正常邮件————判断错误！————其实是垃圾邮件哒!   
正常概率VS错误概率：-54.79272850055003 -55.26584135501914

其中70\73都比较特殊，其邮件字数都很少，难以分类成功

image-20200416172425856

理论上来说，对于贝叶斯而言：

主要优点有：

1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。

2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。

3）对缺失数据不太敏感，算法也比较简单，常用于文本分类。

主要缺点有：

1） 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下，假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。

3）由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。

4）对输入数据的表达形式很敏感。

而综合实验：

对于邮件分类任务而言，贝叶斯确实蛮稳的，在如此少量的数据集中，有稳定的、有效的分类效率，对小规模的数据表现很好。

而其在这个数据集中的准确率ACC最高可达94%，基本无法再提高。

我个人认为原因主要有如下几点：

  • 训练集不够多，不够贴近实际
  • 测试集存在特殊情况，如邮件极短、邮件较独特等
  • 用于训练的特征项数，我上面的实验已经得出了结论

总结

这次的实验还是收获很多的：

  • 学会了使用jieba库进行分词，提取特征词
  • 学会了使用gensim进行word2vec词向量话
  • 最大的收获是，自己实操，对贝叶斯算法进行了一次深入的尝试，很愉悦~
  • 对文本分类的流程、机器学习的理解更深了