2020-04-30-algorithm-homework-2

发表于 | 分类于
字数统计: 3.7k字 | 阅读时长 ≈ 14分钟

1.明显倒置问题——分治

image-20200427220820331

1.1 描述算法思想

我们可以再归并排序的基础上来计算明显倒置。

  • 分治：将一列数字平分为左右两列数字
  • 治理：左右两列数字分别计算其明显倒置个数A、B
  • 合并：计算左列右列（i在左列，j在右列）所含的明显倒置个数C，A+B+C即为明显倒置的总个数

1.2 写出算法伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
def MS_OI(lists):  #merge_sort_Obvious_inversion
    if len(lists) <= 1: #若list个数小于一，直接返回
        return lists,0
    middle = len(lists)/2	#mid是向下取整的数组中间指针
    left,numA = MS_OI(lists[:middle]) #计算有序左数组，以及左数组明显倒置个数
    right,numB = MS_OI(lists[middle:]) #计算有序右数组，以及右数组明显倒置个数
    lists_sort,numC=merge_OV(left, right)#计算有序list，以及左列右列数组明显倒置个数
	return lists_sort,(numA+numB+numC)   #返回有序list，以及总明显倒置个数

def merge_OV(left, right):
    num=0
    c = []  #合并结果数组
    i = j = 0
    left_R=len(left)-1  #left数组最右边元素的下标，这里-1是因为python的数组从零开始
    while i < len(left) and j < len(right):
        if left[i] < right[j]:  #如果左数组当前元素i小于右数组当前元素j，则不满足“明显倒置”
            c.append(left[i])
            i += 1
        else:					#如果左数组当前元素i小于右数组当前元素j，则满足“倒置”
            if(left[i] > 2*right[j]):  #在满足“倒置”的前提下，还满足“明显倒置”
                num=num+1		#首先对这个明显倒置加1
                #因为在left数组中[i]右边的元素都大于[i]，都与当前的right[j]构成“明显倒置”
                #所以left数组中[i]右边的元素有多少个，num就加多少，即len(left)-i
                num=num+left_R-i
            c.append(right[j])
            j += 1

    if i == len(left): #如果left数组已经遍历完，则把right剩下的直接全移到合并数组中
        for x in right[j:]:
            c.append(x)
    else:			   #如果right数组已经遍历完，则把left剩下的直接全移到合并数组中
        for x in left[i:]:
            c.append(x)
    return c,num


if __name__ == '__main__':
    a = [4, 7, 8, 3, 5, 9]
    lists_sort,num=MS_OI(a) #计算num
    print(num)

1.3 分析算法时间复杂度

时间复杂度与归并排序的相同，都为nlog(n)

image-20200427225822702

2.工作最优安排问题——动态规划

image-20200427225957321

2.1 描述算法思路

这道题和我们之前做的 阿里面试题之求括号数、求走楼梯的方法数类似，都是一个数组内的线性规划问题。

我们用一个数组OPT来表示这道题，数组值对应各天最优解，明显是满足最优子结构的。

  • 首先计算0到2天的最优值，即两天之内的情况都工作不用休息
    • OPT[0]=0、OPT[1]=w[1]、OPT[2]=w[1]+w[2]
  • 我们从i=3->k来遍历计算这个数组，对于每个OPT[i]，有三种情况：
    • 1天前的最优值+1天休息：OPT[i]=OPT[i-1]
    • 2天前的最优值+1天休息+1天工作：OPT[i]=OPT[i-2]+w[i]
    • 3天前的最优值+1天休息+2天工作：OPT[i]=OPT[i-3]+w[i-1]+w[i]

2.2 OPT(k)递推式

1
2
3
4
# OPT(0)=0
# OPT(1)=w[1]
# OPT(2)=w[2]
OPT(k)=max(OPT(k-1),OPT(k-2)+w[k],OPT(k-3)+w[k-1]+w[k])

2.3 写出算法伪代码

1
2
3
4
5
6
7
8
9
10
11
def work_arrange(w)
	OPT=[len(w)]
    if len(w)>=1:	 #一天（含）以上的OPT安排	
        OPT[0]=w[0]  #w[0]是工作第0天工作的工资，为零
        OPT[1]=w[1]
    elif len(w)>=2:	 #两天（含）以上的OPT安排
        OPT[2]=w[2]
    else:			#三天（含）以上的OPT安排
        for i=3 to len(w):  #对于三天以上的每天，都有三种情况
            OPT[i]=max(OPT[i-1],OPT[i-2]+w[i],OPT[i-3]+w[i-1]+w[i]) 
    return OPT

2.4 分析算法时间复杂度

O(n)，根据伪代码可知，我们的代码时间复杂度与n成正比。

直接证明法：推导递推式T(n)=T(n-1)+O(1)=T(n-2)+O(1)+O(1)=……=O(n)

数学归纳法证明：

  • 当n=0、1、2时，算法时间复杂度为O(n)
  • 设当n=k时，算法时间复杂度为O(k)=O(n)。而当n=k+1时，算法时间复杂度等于O(k)+O(1)=O(k+1)=O(n)

得证时间复杂度为O(n)

3.棋盘硬币收集问题——动态规划

image-20200427232332542

3.1 描述算法思路

以下 列即x坐标，行即y坐标

x+1往右，y+1往上

自顶向下遍历棋盘的行。

  • 首先计算第n行的所有格子的总价值，因为是最高的棋子，所以总价值就是自身价值。
  • 然后计算第n-1行的总价值，第n-1行的每个格子的总价值计算公式如下：
    • 若是第1列：OPT(x,y)=max(OPT(x,y+1),OPT(x+1,y+1))+c(x,y)
    • 若是第n列：OPT(x,y)=max(OPT(x,y+1),OPT(x-1,y+1))+c(x,y)
    • 其余列：OPT(x,y)=max(OPT(x,y+1),OPT(x-1,y+1),OPT(x+1,y+1))+c(x,y)
  • 同上，自顶向下遍历行计算，最终，得到全棋盘格子可收集最大硬币总价值。

⭐由于考虑到题目仅仅只计算底部任意一个格子的最大总价值，如下图：影响到OPT(x,y)的，仅仅是两条红色线以上的格子。所以我们可以在上述算法上做一点点修改，遍历行时可减少遍历格子数。可降低时间复杂度、提高计算效率。

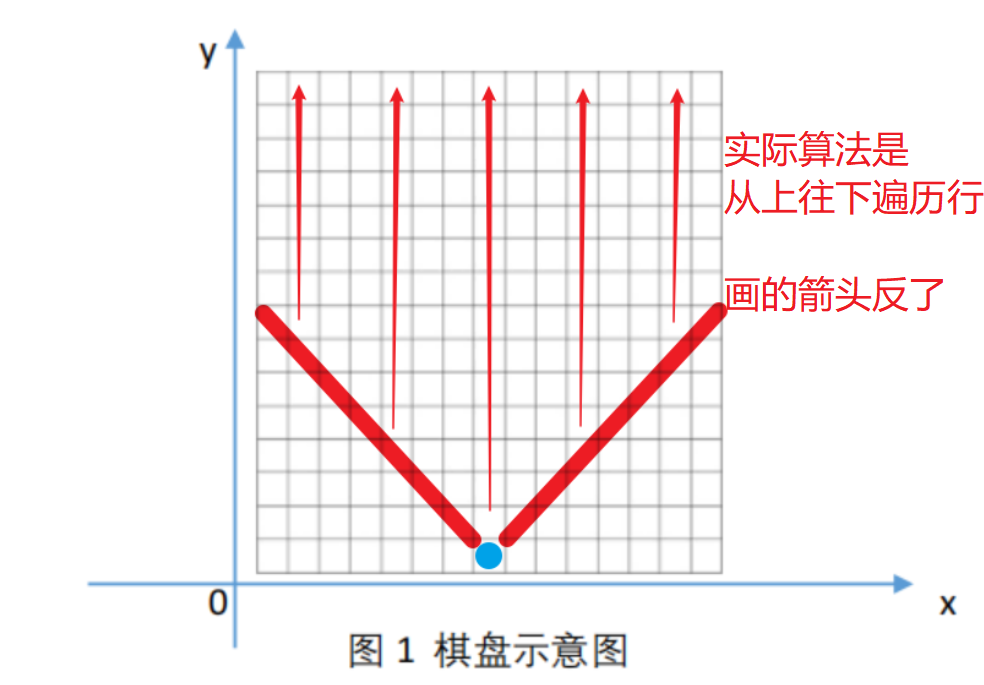
image-20200430172622350

⭐由于题目可在最顶部任意一排格子结束，对于这个要求，我们同样只要加个约束就好了。

3.2 OPT(x,y)递推式

  • 若是第0列：OPT(x,y)=max(OPT(x,y+1),OPT(x+1,y+1))+c(x,y)
  • 若是第n列：OPT(x,y)=max(OPT(x,y+1),OPT(x-1,y+1))+c(x,y)
  • 其余列：OPT(x,y)=max(OPT(x,y+1),OPT(x-1,y+1),OPT(x+1,y+1))+c(x,y)

3.3 写出算法伪代码

以下下标，均是以python数组下标从零开始为前提。range(n)=[n-1,……,0]。

列=x=i，行=y=j

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def CHESS_COIN(c):
    lenc=len(c)
    OPT=[lenc][lenc]
#这是上半部分初始化最高行的代码：
    for i in range(lenc):    #遍历最高行(y)的每列(x)，从0~n-1
		 OPT(i,lenc-1)=(i,lenc-1)
#这是下半部分遍历计算的代码：
    for j in range(lenc-1:0):  #遍历行(y)，从n-2~0
        for i in range(lenc):  #遍历列(x)，从0~n-1
            if i==0 :		 #最左列
                OPT(i,j)=max(OPT(i,j+1),OPT(i+1,j+1))+c(i,j)
            elif i==n-1:	#最右列
                OPT(i,j)=max(OPT(i,j+1),OPT(i-1,j+1))+c(i,j)
            else:			#其余列
            	OPT(i,j)=max(OPT(i,j+1),OPT(i-1,j+1),OPT(i+1,j+1))+c(i,j)
    return OPT

⭐为了使达到题目中的要求： 你可以选择在在最底部一排的任意格子开始，在最顶部一排的任意格子结束

  • 我们在遍历最顶部行时，做一个条件判断是否为最后一个格子（第M列）
1
2
3
4
5
#这是上半部分初始化最高行的代码：
    for i in range(M):    #遍历最高行(y)的每列(x)，从0~M-1
		 OPT(i,lenc-1)=(i,lenc-1)
    for i in range(M:n-1):  #遍历最高行(y) 在M~n-1列的值
        OPT(i,lenc-1)=0
  • 我们在遍历行时要考虑函数是否在红线范围内，判断是否大于直线的值即可，
  • 设最底行的格子坐标为（a,b）这里写个伪代码：

image-20200430172619021

3.4 分析算法时间复杂度

⭐直接证明：

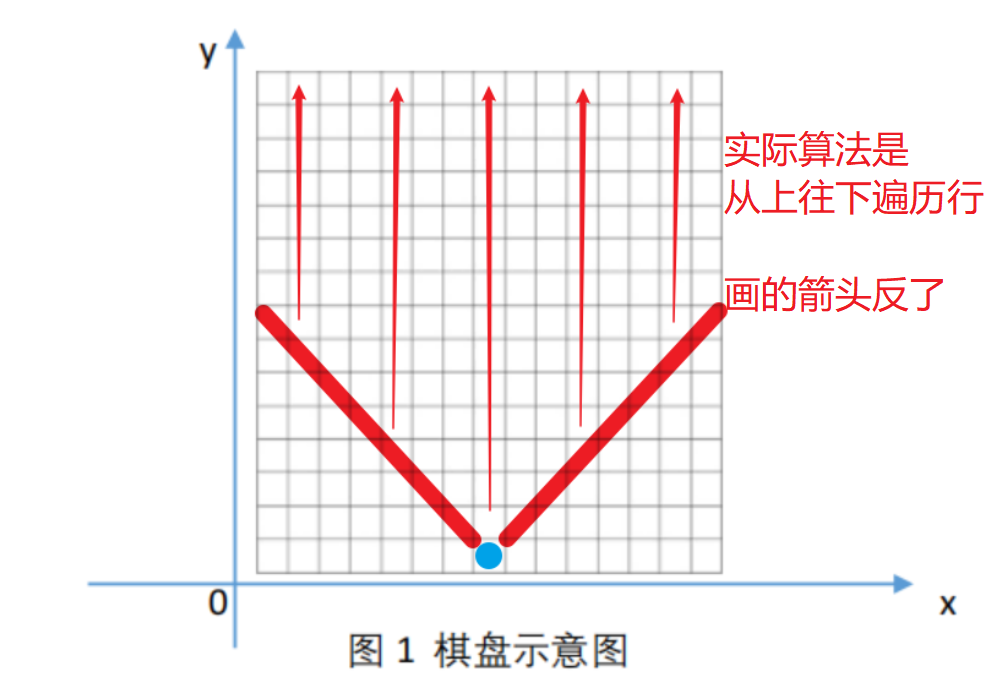
  • 对于题目——棋盘硬币收集问题来说，想要获得一个最底部的格子的最大价值，最少必须要遍历其上方的格子数= n^2 - (1/4)n^2 =(3/4)n^2 。即(3/4)n^2 <=f(n) <= n^2 。

  • 存在正的常数C=1和自然数n0=1，使得当n≥n0时， 有f(n)≤g(n)=n^2。

  • 则称函数f (n) 在n 充分大时有上有界，且g(n) 是它的一个上界，记做f (n) = O(g(n))=O(n^2)

⭐数学归纳法证明：

  • 当n=1时，算法时间复杂度为O(n^2)
  • 设当n=k时，算法时间复杂度为O(k^2)=O(n^2)。而当n=k+1时，算法时间复杂度等于O((k+1)^2)=O(n^2)

得证时间复杂度为O(n^2)

3.5 证明不存在最差时间复杂度为小o(n^2)的动态规划算法

image-20200430172833186

反证法：

  • 假设存在一个动态规划算法的最差时间复杂度为小o(n^2) ，即f(n)=o(g(n)) 。

  • 即0<=f(n)<=cg(n)对于任意常量c>0成立（n>=n0）。

  • 但是，对于题目——棋盘硬币收集问题来说，想要获得一个最底部的格子的最大价值，最少必须要遍历其上方的的格子数= n^2 - (1/4)n^2 =(3/4)n^2 。假如此时取c取1/2，则0<=f(n)<=(1/2)g(n)不成立，矛盾。

  • 反证得不存在最差时间复杂度为小o(n^2)的动态规划算法，最优的算法时间复杂度只能是 大O(n^2)。

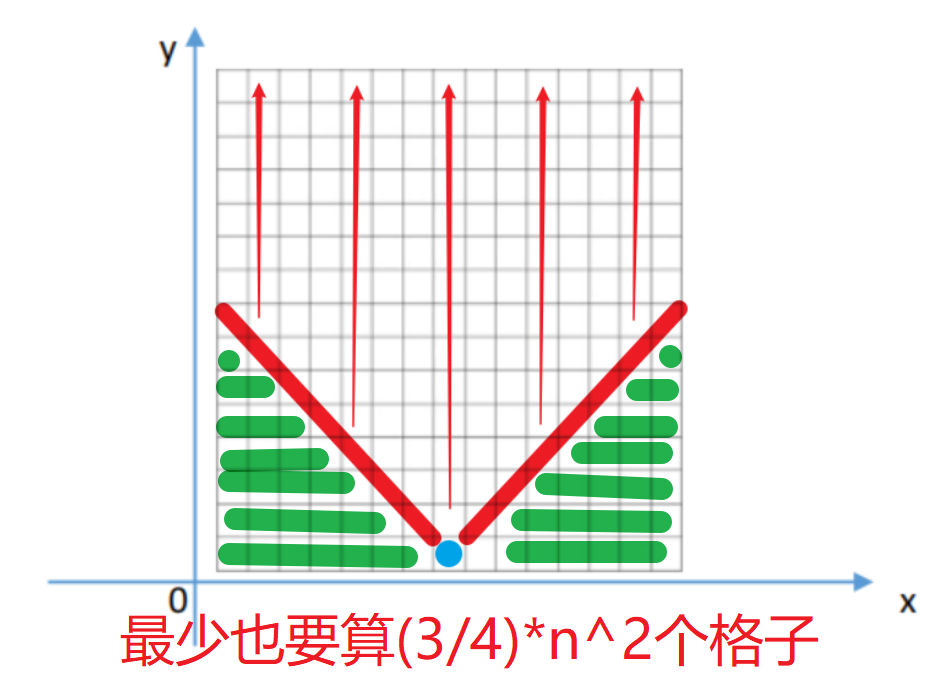
image-20200429180827475

4.dijkstra算法流程图——贪心

image-20200427234432154

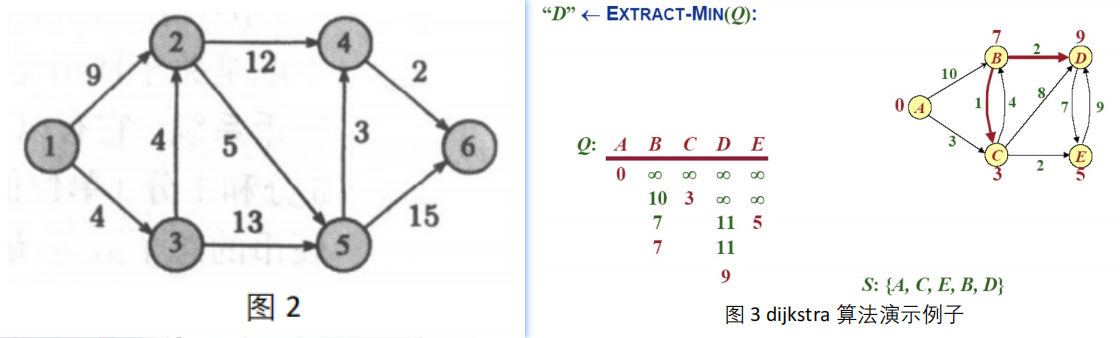
image-20200427234429347

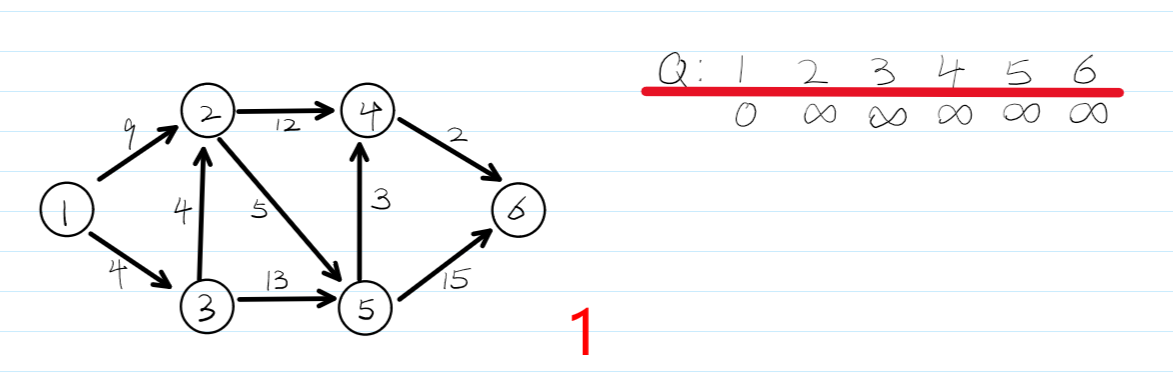
image-20200429171527226

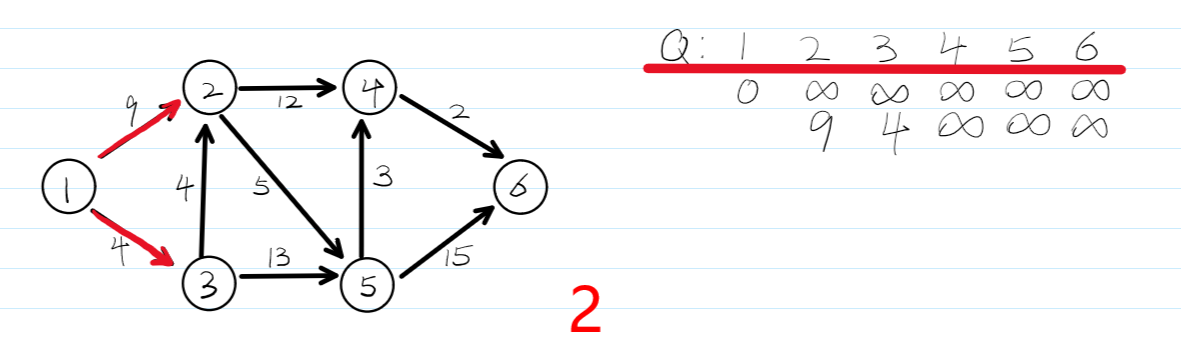
image-20200429171618826

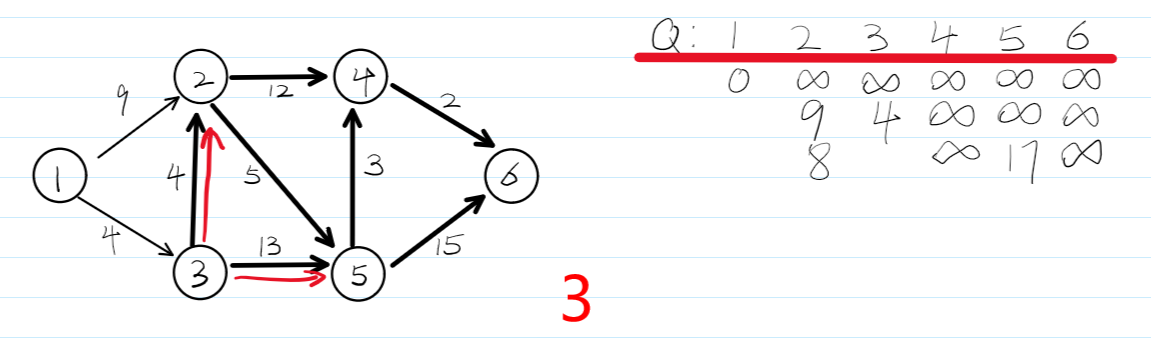
image-20200429171955315

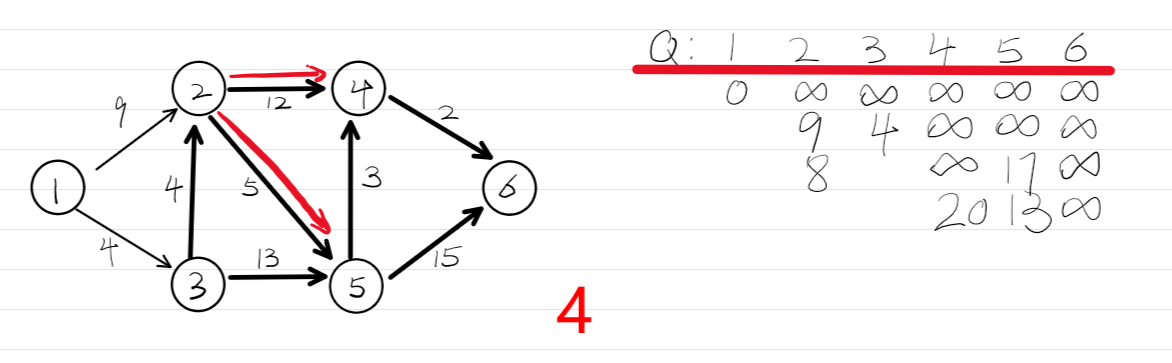
image-20200429172049824

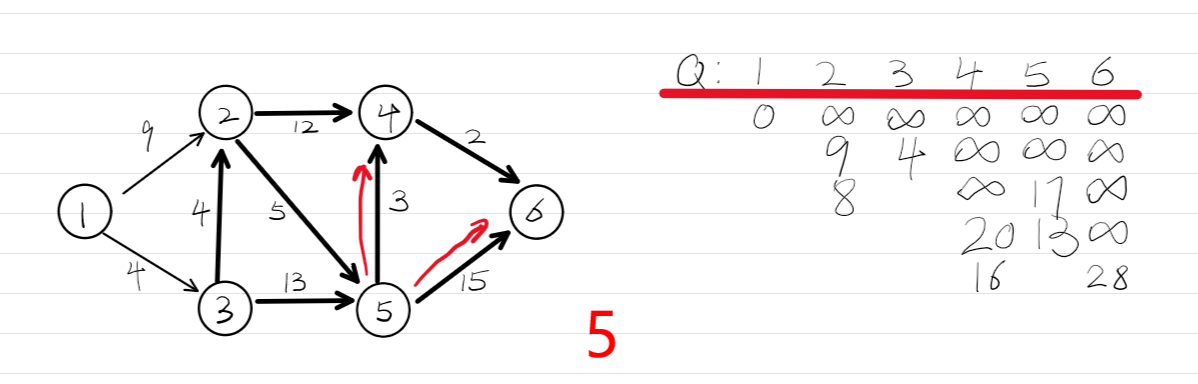
image-20200429172142515

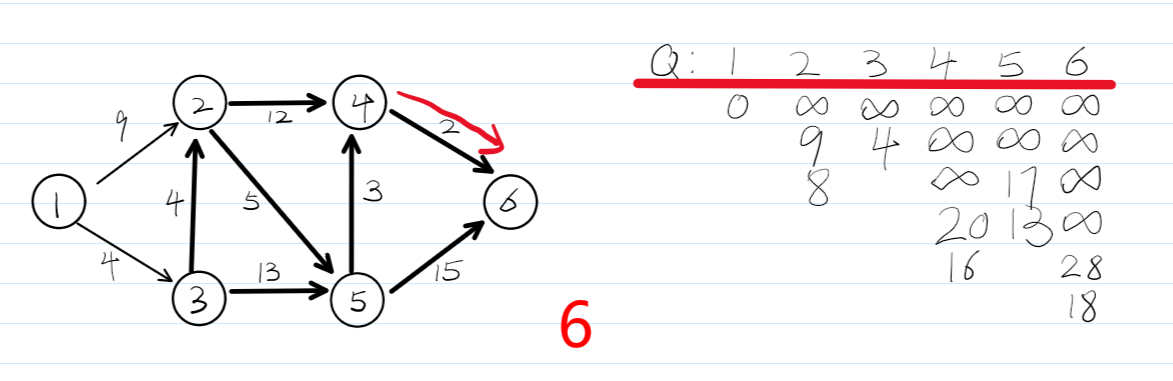
image-20200429172219858

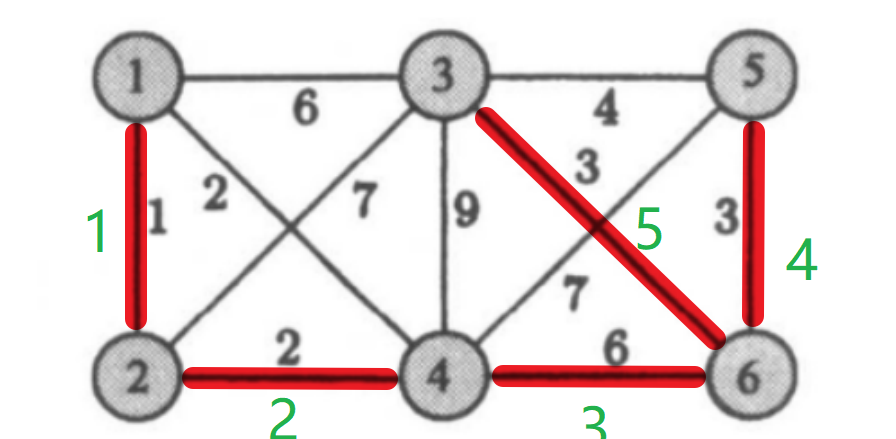
5.kruskal\prim最小生成树——贪心

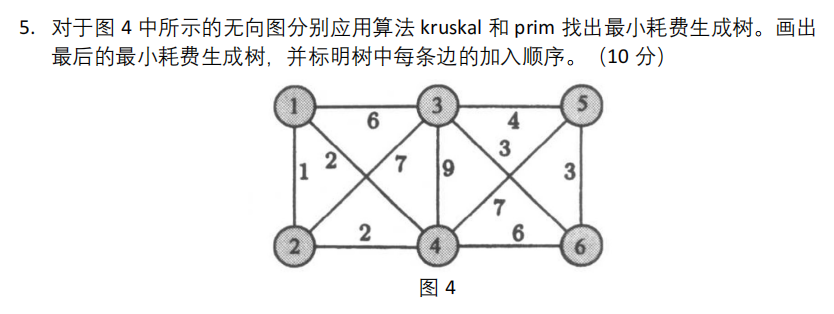
image-20200427234524430

5.1 Kruskal

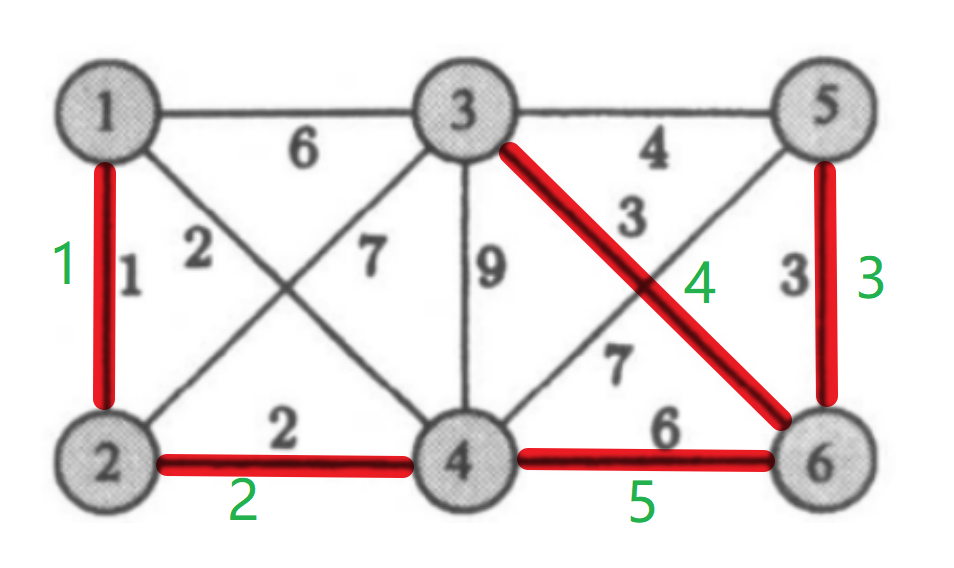
image-20200429173903200

5.2 prim

image-20200429173645486

6.环内活动安排问题——贪心

image-20200427234616837

6.1 描述算法思想

该题，是一个环内的活动安排问题。我们可以遍历每个活动，将该活动从环中去除，余下的时间不成环，为普通活动安排问题。最后比较所有情况求得最优解。我们还可以用以下分类的方法，来减少一些计算量。

考虑以下两种情况下的安排，并且从这些安排中选出最优的。

  • 最优的安排里没有过夜的活动，是一个0-24点的普通活动安排问题。
  • 最优的安排里有过夜的活动，遍历过夜活动集每个过夜活动，剩下的也是普通活动安排问题。

⭐其实，对于过夜的活动，我们还可以用一些小的技巧来减少计算量。但因为计算包含关系有时复杂度会很高，这里当作一个变式。

  • 若过夜活动两两不存在包含关系，则遍历计算，选择最优的安排。
  • 对于活动A在活动B包含下的（即B开始早于A，结束晚于A，真子集关系），直接选择活动A。

6.2 分析算法时间复杂度

考虑以下两种情况下的安排，并且从这些安排中选出最优的。

  • 首先以结束时间为基准，使用冒泡排序0am~24pm的活动。——O(nlogn)

  • 遍历记下过夜的活动在排序数组中的位置，并且用一个数组将保存过夜活动——O(n)

  • 最优的安排里没有过夜的活动，是一个0-24点的普通活动安排问题，得到结果A。——O(n)

  • 最优的安排里有过夜活动，遍历每个过夜活动，剩下的也是普通活动安排问题，寻找该过夜活动(如下)—O(n)

    • tips：对于活动A在活动B包含下的（即B开始早于A，结束晚于A，真子集关系），直接选择活动A。若过夜活动两两不存在包含关系，则遍历计算值，选择最优的安排。但是此操作会增加时间复杂度，可以作为变式使用。

  • 得到一个需要遍历的过夜活动集，遍历过夜活动集每个过夜活动。然后把它所占的区间从0-24小时中去除，然后从这个区间内使用普通活动安排方法计算，得到结果B、C、D……。——O(n^2)

  • 最后，对比几种情况A、B、C……选择最优值（最多活动）。——O(n)

综上，一般情况下，算法时间复杂度为O(n^2)。

6.3 证明算法正确性

（1）贪心选择性质：

  • 对于不含跨夜活动的活动安排。是一个0~24小时普通活动的贪心选择：

    1. 证：假设，存在一个最优解A（不含跨夜活动情况下），且A中的活动也按结束时间非递减排序。A中的第一个活动是K。（设从零点开始的最早结束的活动为F）

    2. 如果K是F，那A就是从0点开始的贪心选择。

      如果K不是F，那么设B=A-{K}∪{F}，因为F早于K结束，且A中的活动是相容的。所以B中的活动也是相容的。又由于B中的活动个数与A中的活动个数相同，故A是最优的，即B是以F开始的最优活动安排。

    3. 所以，最优解A必包含F。

  • 对于含跨夜活动的活动安排：

    1. 证：假设，含某跨夜活动X的最优解为A，且A中的活动也按结束时间非递减排序。A中的第一个活动是K。

      （设F是X结束后开始的结束最早的活动安排）

    2. 如果K是F，那A就是去掉X所占区间后，从X结束时间开始的贪心选择。

      如果K不是F，那么设B=A-{K}∪{F}，因为F早于K结束，且A中的活动是相容的。所以B中的活动也是相容的。又由于B中的活动个数与A中的活动个数相同，故A是最优的，即B是以F开始的最优活动安排。

    3. 所以，最优解A（含某跨夜活动X），是去掉X后，从X结束时间开始的普通活动安排贪心选择。

  • 对于两种类型的解，我们贪心选择活动数量最多的解。

（2）最优子结构性质：

  • 对于不含跨夜活动的活动安排。是一个0~24小时普通活动的贪心选择：
    • 反证法：假设A是活动集E最优解，A中第一个活动是K。设E去掉K后为E’，A去掉K之后为A’。
    • 若E’中存在另一个解B‘ ，比A’有更多的活动，则将K加入B’中产生了另一个解B。这个B将比A拥有 更多的活动，与A的最优性矛盾。故最优解A去掉第一个活动K后，其子结构也是最优的。
  • 对于含跨夜活动的活动安排，同上。
  • 对于以上两种解，我们总是选择的全局最优解，包含了子结构的的最优解。